Altillo.com
> Exámenes > UNLU
> Matemática I
1
EXAMEN FINAL DE MATEMÁTICA I. 19 DE FEBRERO DE 2014 (RESUELTO)
1 a) Resolver analíticamente el sistema :
![]()
![]()
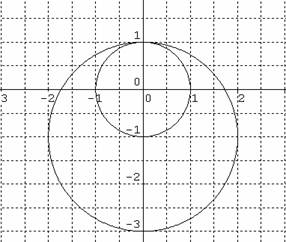
Rta: Único punto de intersección (x, y) = (0, 1)
b) Representar gráficamente las curvas del sistema anterior
2. Hallar el valor de k para que los vectores (0, 1, -2), (k, 1, -1) y (-3, 2, 1) constituyan una base de
![]() . Justificar.
. Justificar.
Debe ser el determinante distinto de cero, para que resulten linealmente independientes:
![]()
![]()
Rta.: k
![]() -3/5. Constituyen una base de
-3/5. Constituyen una base de
![]() porque son tres vectores de
porque son tres vectores de
![]() , linealmente independientes.
, linealmente independientes.
3. Escribir las ecuaciones cartesianas del subespacio de
![]() de dimensión 1 que es perpendicular al plano
de dimensión 1 que es perpendicular al plano
![]()
El subespacio es la recta de
![]() : X = t (2, -1, 1). La matriz
: X = t (2, -1, 1). La matriz
![]() tiene rango 1. Luego
tiene rango 1. Luego
![]() = 0,
= 0,
![]()
Rta: Las ecuaciones cartesianas son: -x - 2y = 0, x -2z = 0.
4. Dada A =
![]() a) Investigar, sin resolverlo, si el sistema A.X = 0 tiene solución única. Justificar.
a) Investigar, sin resolverlo, si el sistema A.X = 0 tiene solución única. Justificar.
Det. (A) =
![]() = 0
= 0
Rta.: El sistema A.X = 0 no tiene solución única porque el det. (A) es nulo.
b) Hallar una base del espacio de soluciones del sistema del ítem a).
![]()
![]()
Dimensión = n – r = 3 – 2 =1. Base de 1 vector. La solución del sistema es (z, z, z).
Rta: una base es:
![]()
5. Indicar, en cada caso, si el conjunto de vectores es linealmente dependiente o independiente.
Justificar.
![]() Rta.: Son 3 vectores de
Rta.: Son 3 vectores de
![]() , 3
, 3
![]() , por teorema los vectores son linealmente
dependientes.
, por teorema los vectores son linealmente
dependientes.
b)
![]()
![]() r = 2. Rta: Los vectores son linealmente independientes.
r = 2. Rta: Los vectores son linealmente independientes.
c)
![]()
![]() Rta: Los vectores son linealmente
independientes.
Rta: Los vectores son linealmente
independientes.
d)
![]() Rta: Por Convención un vector
Rta: Por Convención un vector
![]() es siempre linealmente independiente.
es siempre linealmente independiente.
6. a) Calcular la dimensión del subespacio de
![]() generado por los vectores A = (0, 1, -2),
generado por los vectores A = (0, 1, -2),
B = (1, -1,-2) y C = (-1, 2, 0).
C = A – B, pero A y B son linealmente independientes; por lo tanto la dimensión es 2.
b) Escribir la ecuación cartesiana de dicho subespacio.
![]() Rta: 4x +2y +z =0.
Rta: 4x +2y +z =0.
7. Escribir la ecuación vectorial de la intersección de los siguientes planos de
![]() :
:
![]()
![]()
![]()
Rta: X = u (1/2, 1, 0) + v (-3/2, 0, 1) u y v reales arbitrarios.
8. a) Definir subespacio de un espacio vectorial real. Ver libro del Dr. Novelli, Cap. III.
b) ¿El conjunto de todos los vectores (x, y, z) de
![]() tales que x +2y = 0, x –y = z -2 es un
tales que x +2y = 0, x –y = z -2 es un
subespacio de
![]() ? Justificar.
? Justificar.
Rta: No es un subespacio porque en el conjunto no está el vector nulo.
Sólo para alumnos libres
9) Demostrar que si A es una matriz de orden n, tal que existe
![]() , entonces det (
, entonces det (
![]() ) =
) =
![]()
Demostración: En efecto, A.
![]()
det(A.
![]() ) = det. (I), como el det.de un producto es el producto de
) = det. (I), como el det.de un producto es el producto de
los det. , resulta det.(A) . det.(
![]() , y entonces
, y entonces
det(
![]() ) =
) =
![]()