Altillo.com > Exámenes > UBA - CBC > Análisis

1. Sea Bn una sucesión tal que Bn > (1,4)ⁿ para todo n >=30
Calcular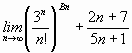

2. Sea F(x) = 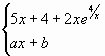    si    
Hallar a y b para qeu F sea derivable en x = 0

3. Demuestre que 2x+Ln (1+ 4x)>= 5x - 8x² para todo x >= 0

4. Sea f: [0,1] -------> R definida por F(x)= x / (3x² + 1). Dados los puntos A=(1,0) , B=(x,0) , C=(x,F(x)) (x E [0,1] ), hallar las coordenadas del punto C para qeu el area del triangulo ABC sea Maxima. Dar las razones que permitan asegurar que el triángulo hallado es efectivamente el de área máxima.

Respuestas
1) 2/5 para todo n>=30
2) A=5 , B=4
3) Hay que pasar todo para el mismo lado de la ecuacion y qeu qeude una
desigualdad a cero y demostrar qeu pasa eso siempre.
4) A=(1,0) B=(1/3,0) C=(1/3,1/4)