Altillo.com > Exámenes > UBA - CBC > Análisis

1) Sea una función que satisface la siguiente ecuación integral

donde h es una función cuyo polinomio de Taylor de orden 2 en x = 1 es p(x) = 3 - 2(x - 1) + 5(x - 1)². Encuentre el polinomio de Taylor de orden 2 en x = 1 de f.

2) Encuentre una función sabiendo que f(0) = 2 y tal que f(x) , f '(x) = 2x² + 3.

3) Calcule el área comprendida entre los semiejes positivos, la curva y la recta tangente a dicha curva en x = 5, de ecuación .

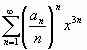4) Sea (a_n) una sucesión de números positivos tal que . Halle el radio de convergencia de la serie . Indique, en cada caso, las propiedades y criterios que usa para obtener sus conclusiones.

Respuestas
1)
2)
3)

4)