| An�lisis Matem�tico 1 | Examen Final | 2 / 03 / 2002 | Altillo.com |
1) Dada ![]() indique si las siguientes afirmaciones son verdaderas (V) o falsas (F). Si
son verdaderas justifique su respuesta y si son falsas de el resultado correcto:
indique si las siguientes afirmaciones son verdaderas (V) o falsas (F). Si
son verdaderas justifique su respuesta y si son falsas de el resultado correcto:
![]() c)
c) ![]() .
.
3) Determine si cada una de las siguientes afirmaciones es verdadera o
falsa. Justifique su respuesta.
a) Si 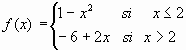 y
y ![]() entonces
entonces 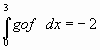
b) Dada ![]() su intervalo de convergencia es abierto.
su intervalo de convergencia es abierto.
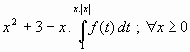 y la ecuaci�n de la recta tangente a la gr�fica de f en x = 1 es
y + 4x �2 = 0. Obtenga el polinomio de Taylor de segundo grado asociado a la
funci�n g en potencias de (x-1).
y la ecuaci�n de la recta tangente a la gr�fica de f en x = 1 es
y + 4x �2 = 0. Obtenga el polinomio de Taylor de segundo grado asociado a la
funci�n g en potencias de (x-1).
5) Estudie la continuidad y derivabilidad de las funciones f
, f � y f �� . Siendo ![]() .
Justifique su respuesta.
.
Justifique su respuesta.
Condici�n m�nima para aprobar: 50% del examen bien resuelto.