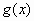 continua y derivable en
continua y derivable en 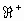 tal que
tal que 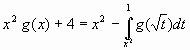 si sabe que
si sabe que
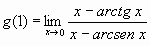
| An�lisis Matem�tico 1 | Examen Final | 12 / 02 / 2002 | Altillo.com |
1) Determine la funci�n 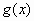 continua y derivable en
continua y derivable en 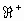 tal que
tal que 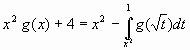 si sabe que
si sabe que
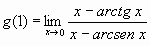
2) Indique si cada una de las siguientes afirmaciones es
verdadera o falsa. En cada caso justifique su respuesta.
a) "Si 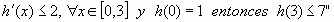
b) "Si la ecuaci�n de la recta tangente a la gr�fica de f
en x= -1 es y + 5x - 3 = 0, entonces la ecuaci�n de la recta tangente al
gr�fico de 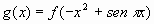 en x=1
es
en x=1
es ![]()
3) Pruebe que "Si la funci�n h admite en x=a un extremo local y existe h�(a) entonces h�(a)=0". �Es v�lido el rec�proco del enunciado anterior? Justifique.
4) El n�mero positivo A es el valor del �rea
limitada por la gr�fica de 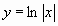 e
e ![]() .
.
Determine el polinomio de Taylor de tercer grado en 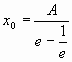 de f(x) = arctg x.
de f(x) = arctg x.
5) Si 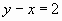 es la ecuaci�n de la recta tangente al gr�fico de
es la ecuaci�n de la recta tangente al gr�fico de 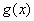 en
en 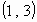 y
y 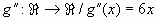 ,
entonces determine la funci�n g.
,
entonces determine la funci�n g.
Condici�n m�nima para aprobar
: 50% del examen bien resuelto