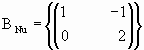Altillo.com > Exámenes > UTN > Algebra y Geometría Analítica

Algebra y Geometría Analítica Examen Final (Con Respuestas) 2do Cuat. de 2006 Altillo.com

1) Sea la recta

a. Halle el área del triángulo cuyos vértices son las intersecciones de la recta con los planos coordenados y el origen de coordenadas.

b. Halle la ecuación del plano que contiene a la recta r y al origen de coordenadas. Grafique el plano.

2)

a. Sea el plano . Halle el radio R de una esfera de centro en C(4;-3;2) tal que la intersección entre el plano y la esfera sea una circunferencia de radio r=3 ¿Cuál es el centro de la circunferencia? ¿Cuál es la ecuación de la esfera?

b. Identifique la superficie en cada uno de los siguientes casos:

i. A=C=1B=-1L=1

ii. A=1B=0C=-1L=0

3)

a. Justifique si la siguiente afirmación es verdadera o falsa

Si A (N matriz nula)

b. Si A, donde Ai es la i-ésima columna de la matriz A. Halle kR tal que siendo

4) Halle la matriz asociada a la transformación lineal respecto a las bases canónicas en R3 sabiendo que dicha matriz tiene a l=2 como autovalor asociado al autoespacio , y que T(1;0;0)=(-1;0;0)

5)

a. Sean los subespacios vectoriales de :

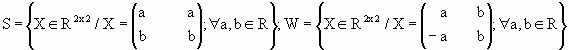
Halle base de S y de W y obtenga SW y S+W ¿es suma directa?

b. Sea la transformación lineal

Halle Nu(T), Im(T), base de cada uno de ellos.

Respuestas:

1)a. Vértices O(0;0;0), A(0;0;1) y B 1.b. 4x+y=0

2)a.

2)b.i. Hiperboloide de una hoja de revolución de eje //ejey

2)b.ii. Dos planos x-z=1; x+z=1

3)a. verdadero 3.b.

4)

5)a.

(entonces la suma es directa)

S+W=R2x2

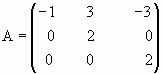
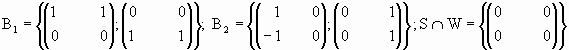
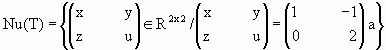5)b. ; Im(T)=R3

; BIm={(1;0;0);(0;1;0);(0;0;1)}