Altillo.com > Exámenes > UBA - CBC > Análisis

1_a) Halle el polinomio de Taylor de orden 3 de alrededor del punto .
    b) Sabiendo que , encuentre una cota para el resto .

2) Sea 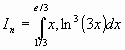. Pruebe que .

3) Considere la región comprendida entre la curva , la recta x = 1 y la recta y = x - a (con 0 < a < 1). Halle el valor de a para el cual el área de la región sea igual a .

4) Halle el valor de k > 0 para que la serie sea convergente si y solamente si . Para el valor de k hallado muestre que si la serie no converge. Explique las propiedades y criterios que usa para obtener sus conclusiones.

Respuestas
1_a)
    b)
2)
3) -
4) k = 9