.
En caso de no existir el l�mite, justificar adecuadamente la respuesta.Altillo.com > Ex�menes > UBA - CBC > An�lisis
|
An�lisis |
1� Parcial |
Tema 4 |
2� Cuat. 1998 |
Altillo.com |
1) Calcular, si existe, .
En caso de no existir el l�mite, justificar adecuadamente la respuesta.
2) Mediante el estudio de los cocientes incrementales, estudiar la
derivabilidad de la funci�n f en 
,
siendo
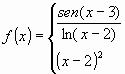
3) Sea 
una funci�n derivable tal que 
y 
Probar que 
4_a) Estudiar m�ximos y m�nimos locales, intervalos de crecimiento y
decrecimiento, concavidades y as�ntotas de 
Hacer un gr�fico aproximado de 
4_b) Hallar un m�ximo valor de 
y el m�nimo valor de 
tales que
Respuestas:
1) 
ya que dos sucesiones no podr�an tener el mismo l�mite
2) No existe el l�mite de 
3) Es siempre positiva, ya que como 
,
es positiva en todo 
.
El valor m�ximo lo deber� tomar en 
,
como ese valor es 
y por lo tanto, la funci�n nunca vale cero en ese intervalo.
4_a) Tiene m�nimo en 1.
Decrece en: 
.
Crece en: 
.
es
convexa.
es
c�ncava.
La as�ntota horizontal es 
.
4_b) La funci�n est� acotada superiormente por 7 e inferiormente por 
,
entonces: 
Contestamos: 
